
Momento de inercia
De Wikipedia, la enciclopedia libre
El momento de inercia o inercia rotacional es una magnitud que da cuenta de cómo es la distribución de masas de un cuerpo o un sistema de partículas alrededor de uno de sus puntos. En el movimiento de rotación, este concepto desempeña un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme. Representa la inercia de un cuerpo a rotar.
Tabla de contenidos |
[editar] Definición de momento de inercia
El momento de inercia (escalar) de una masa puntual rotando alrededor de un eje conocido se define por
donde
- m es la masa del punto, y
- r es la distancia mínima entre ella y el eje de rotación.
Dado un eje arbitrario, para un sistema de partículas se define como la suma de los productos entre las masas de las partículas que componen un sistema, y el cuadrado de la distancia r de cada partícula al eje escogido. Matemáticamente se expresa como:
Para un cuerpo de masa continua (Medio continuo) lo anterior se generaliza como:
El subíndice V de la integral indica que hay que integrar sobre todo el volumen del cuerpo.
Este concepto, desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme.(La masa es la resistencia que presenta un cuerpo a ser acelerado en traslación y el Momento de Inercia es la resistencia que presenta un cuerpo a ser acelerado en rotación) Así, por ejemplo, la segunda ley de Newton:  tiene como equivalente para la rotación:
tiene como equivalente para la rotación:
donde:
 es el momento aplicado al cuerpo.
es el momento aplicado al cuerpo. es el momento de inercia del cuerpo con respecto al eje de rotación y
es el momento de inercia del cuerpo con respecto al eje de rotación y es la aceleración angular.
es la aceleración angular.
La energía cinética de un cuerpo en movimiento con velocidad v es  , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ? es
, mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ? es 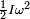 . Donde I es el momento de inercia con respecto al eje de rotación.
. Donde I es el momento de inercia con respecto al eje de rotación.
La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular 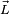 :
:
El vector momento angular tiene la misma dirección que el vector velocidad angular 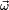 .
.
[editar] Momentos de inercia de algunas figuras interesantes
En estas tablas además de los momentos de inercia de las figuras, podemos encontrar datos interesantes como centro de masas, volumen o area, y producto de inercia.
Imagen:Momentos de inercia 1.jpg Imagen:Momentos de inercia 2.jpg 


[editar] Teorema de Steiner o Teorema de los ejes paralelos
El teorema de Steiner establece que el momento de inercia con respecto a cualquier eje paralelo a un eje que pasa por el centro de gravedad, es igual al momento de inercia con respecto al eje que pasa por el centro de gravedad más el producto de la masa por el cuadrado de la distancia entre los dos ejes:
Donde: Ieje es el momento de inercia respecto al eje que no pasa por el centro de masa; I(CM)eje es el momento de inercia para un eje paralelo al anterior que pasa por el centro de gravedad; M – Masa Total y h – Distancia entre los dos ejes paralelos considerados. La demostración de este teorema resulta inmediata si consideramos la descomposición de coordenadas relativa al centro de masas C  inmediata:
inmediata:
Donde el segundo término es nulo puesto que la distancia vectorial promedio de masa en torno al centro de masa es nula, por la propia definición de centro de masa.
[editar] Tensor de inercia de un sólido rígido
El tensor de inercia de un sólido rígido, es un tensor simétrico de segundo orden, que expresado en una base ortonormal viene dado por una matriz simétrica, cuyas componentes tensoriales son:
Donde:
- (x1,x2,x3)[ = (x,y,z)] son las coordenadas para nombrar a los puntos del cuerpo.
 , es la llamada delta de Kronecker definida como:
, es la llamada delta de Kronecker definida como: 
A los elementos 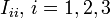 se los llama momento de inercia respecto del eje i y tienen las mismas propiedades que los momentos de inercia considerados anteriormente. Si usamos un sistema de coordenadas cartesiano XYZ y calculamos en ellos el tensor, sus componentes vienen dadas por los tres momentos de inercia siguientes:
se los llama momento de inercia respecto del eje i y tienen las mismas propiedades que los momentos de inercia considerados anteriormente. Si usamos un sistema de coordenadas cartesiano XYZ y calculamos en ellos el tensor, sus componentes vienen dadas por los tres momentos de inercia siguientes:
Y los tres productos de inercia según los mismos ejes:
Todas las formas anteriores pueden resumirse en la siguiente fórmula tensorial:
Donde  y donde
y donde  . El momento con respecto a cualquier otro eje puede expresarse como combinación lineal anterior de las anteriores magnitudes:
. El momento con respecto a cualquier otro eje puede expresarse como combinación lineal anterior de las anteriores magnitudes:
Donde la matriz anterior es el tensor de inercia expresado en la base XYX y t = (tx, ty, tz) es el vector paralelo al eje según el cual se pretende encontrar el momento de inercia.
[editar] Véase también


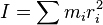


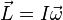

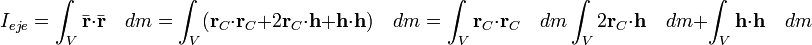

![I_{ij}= I_{ji} = int_M left[ delta_{ij}left(sum_i x_i^2right)-x_ix_j right] dm = int_V rho(mathbf r)left[ delta_{ij}left(sum_{i=1}^3 x_i^2right)-x_ix_j right] quad dx_1dx_2dx_3](https://upload.wikimedia.org/math/5/4/1/5418847b9a885967aa0ee30dc70c60a5.png)
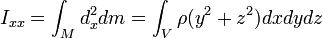
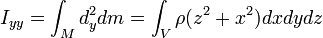


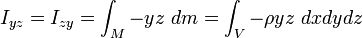

![I_{ij} = I_{ji} = int_V -rho left[left(sum_i x_i^2right)-x_ix_jright] dxdydz](https://upload.wikimedia.org/math/d/f/0/df0a785a87ff9546e04b5a7179fcab1e.png)
