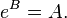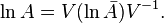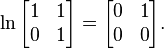Wiki de astronomía.

Todo el poder de la Wikipedia y toda la esencia de la astronomía

Logaritmo de una matriz

De Wikipedia, la enciclopedia libre

En matemática, el logaritmo de una matriz es una función matricial que generaliza el logaritmo escalar a matrices. Es en cierto sentido la función inversa de la exponenciación de matrices.

Tabla de contenidos

1 Definición
2 Propiedades
3 Cálculo de logaritmo
- 3.1 Matriz diagonalizable
- 3.2 Matriz no diagonalizable
4 Véase también

[editar] Definición

Una matriz B es logaritmo de una matriz dada A si la exponenciación de B es A:

$e^B = A. ,$

[editar] Propiedades

Una matriz tiene logaritmo sí y sólo sí es inversible.
No obstante, este logaritmo puede ser complejo aún si todos los valores son números reales.
En cualquier caso, el logaritmo no es único.

[editar] Cálculo de logaritmo

[editar] Matriz diagonalizable

Un método para encontrar $ln A$ para una matriz diagonalizable es el siguiente:

Encontrar la matriz V de vectores propios de A (cada columna de V es un autovector de A).

Encontrar la Matriz inversa V^?1 de V.

Ahora

$bar{A} = V^{-1} A V.,$

Entonces $bar{A}$ será una matriz diagonal cuyos elementos de la diagonal serán valores propios de A.

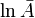Reemplazando cada elemento de la diagonal de A? por su logaritmo natural para obtener $ln bar{A}$ .

Entonces

$ln A = V ( ln bar{A} ) V^{-1}. ,$

Que el logaritmo de A puede ser una matriz compleja aún si A es real una consecuencia del hecho de que una matriz con valores reales puede llegar a tener valores propios complejos (por ejemplo, esto es cierto para las matrices de rotación). La no unicidad del logaritmo de una matriz es consecuencia de la no unicidad del logaritmo de un número complejo.

[editar] Matriz no diagonalizable

El algoritmo ilustrado arriba no funciona para matrices no diagonalizables, como:

$begin{bmatrix}1 & 1\ 0 & 1end{bmatrix}.$

Para este tipo de matrices se necesita encontrar su forma canónica de Jordan y, más que calcular los logaritmos de la diagonal como ocurría para las matrices diagonalizables, uno calcula el logaritmo de los elementos de la matriz de Jordan.

Lo último se logra al notar que uno puede escribir un bloque de Jordan como:

$B=begin{pmatrix} lambda & 1 & 0 & 0 & cdots & 0 \ 0 & lambda & 1 & 0 & cdots & 0 \ 0 & 0 & lambda & 1 & cdots & 0 \ vdots & vdots & vdots & ddots & ddots & vdots \ 0 & 0 & 0 & 0 & lambda & 1 \ 0 & 0 & 0 & 0 & 0 & lambda \end{pmatrix} = lambda begin{pmatrix} 1 & lambda^{-1} & 0 & 0 & cdots & 0 \ 0 & 1 & lambda^{-1} & 0 & cdots & 0 \ 0 & 0 & 1 & lambda^{-1} & cdots & 0 \ vdots & vdots & vdots & ddots & ddots & vdots \ 0 & 0 & 0 & 0 & 1 & lambda^{-1} \ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}=lambda(I+K)$

Dónde K es una matriz con ceros en y debajo de la diagonal. (El número ? no es cero por la suposición de que la matriz cuyo logaritmo uno intenta calcular es inversible.)

Entonces, por la fórmula

$ln (1+x)=x-frac{x^2}{2}+frac{x^3}{3}-frac{x^4}{4}+cdots$

se obtiene:

$ln B=ln big(lambda(I+K)big)=ln (lambda I) +ln (I+K)= (ln lambda) I + K-frac{K^2}{2}+frac{K^3}{3}-frac{K^4}{4}+cdots$

Esta serie en general, no converte para ninguna matriz K, como tampoco lo hace para ningún número real con valor absoluto mayor a la unidad. No obstante, esta matriz K en particular, es una matriz nilpotente, por lo tanto la serie tiene un número finito de términos (K^m es cero si m es la dimensión de K).

Utilizando este enfoque uno encuentra

$ln begin{bmatrix}1 & 1\ 0 & 1end{bmatrix} =begin{bmatrix}0 & 1\ 0 & 0end{bmatrix}.$