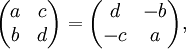Wiki de astronomía.

Todo el poder de la Wikipedia y toda la esencia de la astronomía

Matriz ortogonal

De Wikipedia, la enciclopedia libre

Las matrices ortogonales, representan transformaciones en espacios vectoriales reales^[1] llamadas justamente, transformaciones ortogonales. Estas transformaciones son isomorfimos internos del espacio vectorial en cuestión. Suelen representar rotaciones y son usadas extensivamente en computación gráfica. Por sus propiedades también son usadas para el estudio de ciertos fibrados y en física se los usa en la formulación de ciertas teorías de campos.

[editar] Definición

Sea $n$ un número entero y sea $A$ una matriz cuadrada $n$ por $n$ , con entradas reales. Se dice que la matriz es ortogonal si

$Acdot A^t = mathbb{I}$

donde $A t$ representa la matriz transpuesta de $A$ e I representa la matriz identidad.

[editar] Ejemplos

Supongamos que la matriz de números reales

$M= begin{pmatrix} a & b\ c & d end{pmatrix},$

es ortogonal y su determinante es +1. Su transpuesta es igual a su inversa

$begin{pmatrix} a & c\ b & d end{pmatrix} = begin{pmatrix} d & -b\ -c & a end{pmatrix},$

de modo que $d$ = $a$ y $c$ = $? b$ y la matriz $M$ es de la forma

$M= begin{pmatrix} a & b\ -b & a end{pmatrix}.$

Finalmente,

$Mcdot M^t = begin{pmatrix} a & b\ -b & a end{pmatrix}cdotbegin{pmatrix} a & -b\ b & a end{pmatrix} = begin{pmatrix} a^2 + b^2 & 0\ 0 & a^2 + b^2 end{pmatrix} = begin{pmatrix} 1 & 0\ 0 & 1 end{pmatrix},$

Así que los números $a$ y $b$ satisfacen además la propiedad que la suma de sus cuadrados vale 1. Por lo tanto, existe un número real $?$ para el cual

$a=costhetaquad b=sintheta.$

Concluimos que: toda matriz ortogonal de $S O (2)$ puede escribirse como

$M_theta = begin{pmatrix} costheta & sintheta\ -sintheta & costheta end{pmatrix}$

con $?$ real.

[editar] Caracterización

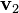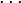
Sea $A$ una matriz ortogonal $n$ por $n$ . Sean $mathbf{v}_1$ , $mathbf{v}_2$ , $cdots$ $mathbf{v}_n$ los $n$ vectores fila de la matriz. En término de estos vectores, es muy fácil expresar los elementos de la matriz que resulta de muliplicar $A$ por su transpuesta:

$(Acdot A^t)_{ij} = mathbf{v}_icdotmathbf{v}_j = delta_{ij} = begin{cases} 1 & mbox{si }i = j, \ 0, & mbox{si }i ne j end{cases}$

De modo que los vectores fila de una matriz ortogonal forman un conjunto de $n$ vectores ortonormales. Puesto que la ecuación

$A^tcdot A = mathbb{I}$

también se verifica, tenemos que los vectores columna de la matriz $A$ también forman un conjunto ortonormal de vectores. Como el recíproco de todo esto también es cierto, tenemos

Una matriz real $A$ es ortogonal si y sólo si sus vectores filas o vectores columna son cada uno un conjunto ortonormal de vectores.

Es en este sentido que se dice que se ha hecho una caracterización de las matrices ortogonales. Dada una matriz, basta verificar esta propiedad entre sus vectores fila y columna para determinar si dicha matriz es o no ortogonal.

[editar] Propiedades

De la definición, es inmediato que la si una matriz es ortogonal, la matriz es no singular o inversible y su transpuesta coincide con su inversa
El determinante de una matriz ortogonal $A$ es +1 ó -1. En efecto, de las propiedades del determinante tenemos

$det(Acdot A^t) = det A det A^t = det A det A = (det A)^2 = detmathbb{I} = 1,$

y por tanto,

$det A = pm 1.$

El conjunto de matrices nxn ortogonales, junto con la operación de producto de matrices es un grupo llamado grupo ortogonal O(n). Supongamos que $A$ y $B$ son matrices ortogonales y sea $C$ igual al producto de $A$ por $B$ . Usando las propiedades del producto de matrices, tenemos

$begin{align} Ccdot C^t &= (Acdot B)cdot(Acdot B)^t = (Acdot B)cdot(B^tcdot A^t)\ & = Acdot ( Bcdot B^t)cdot A^t = Acdot mathbb{I}cdot A^t = A cdot A^t = mathbb{I}, end{align}$

y así, el producto de matrices ortogonales es una matriz ortogonal.

En matemáticas, al grupo de matrices ortogonales

n

por

n

se denomina grupo ortogonal de dimensión

n

y se representa con

O (n)

. En particular el subgrupo formado por las matrices ortogonales de determinante +1, se llama grupo especial ortogonal y se le representa con

S O (n)

. Entre las matrices ortogonales se encuentran las matrices de rotación y las de permutación.

[editar] Notas

? Se sobreentiende que al espacio vectorial real, se le ha dotado de un producto interno

[editar] Véase también

Para profundizar sobre este tema y en general sobre álgebra, pude consultar

G. Birkhoff, S MacLane, Álgebra Moderna, ed. Vicens-Vives, Madrid 1980. ISBN 84-316-1226-6